Surface Area is the amount of space covering the outside of a 3D shape. This math concept allows students to visualize and is concrete, but that doesn’t mean all students will immediately excel. Let’s talk about some of our best tips for teaching surface area of prisms, cylinders, and pyramids.
Standards
Let’s start with the standards. While surface area is covered in 8th CCSS, it spans both 7th and 8th grade in the TEKS.
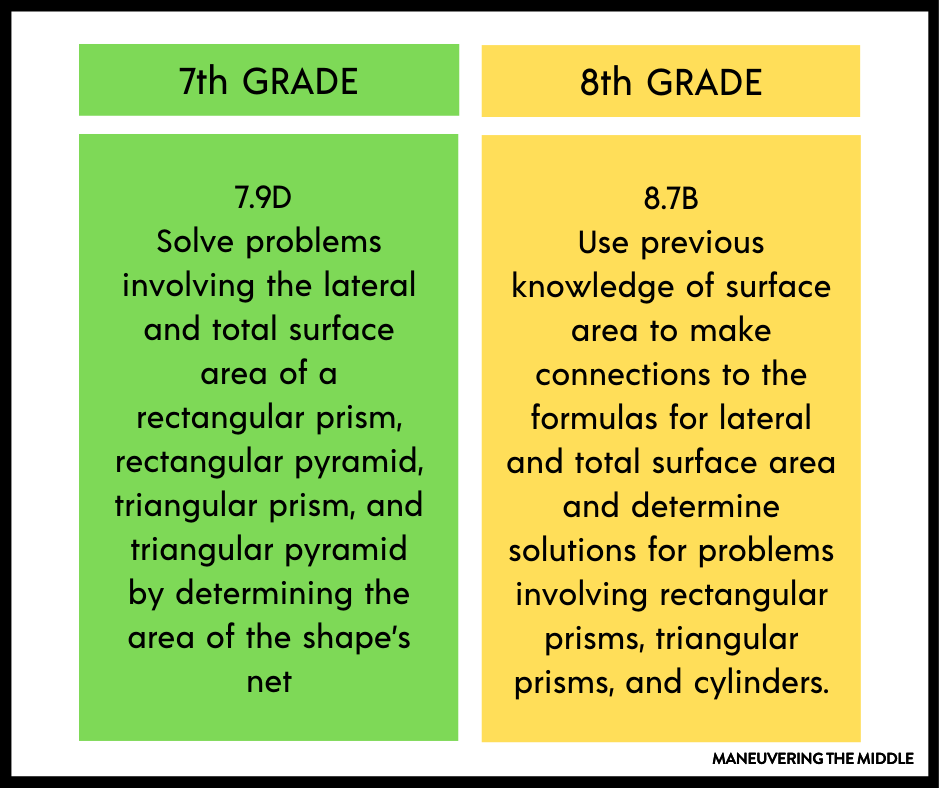
One thing to note is that in 7th grade, students will use a net to determine the surface area of 3D shapes. In 8th grade, students will have access to formulas to solve.
Lateral vs. Total Surface Area
In the standards above, lateral and total surface area are distinct. Students must be able to carefully read a problem and determine if the area of the bases should be included. I have students who would absolutely see the net below and start finding the surface area without even reading whether the question was asking for the lateral or total surface area. A tip here would be to ask students to write “no bases” when they see lateral surface area and draw Xs on the bases.

Problems in which lateral surface area is often seen:
- Surface area of a soup can label
- Surface area of an oatmeal canister
- The amount of square feet covered when rolling a paint roller or rolling pin
- The amount of paint needed to paint the walls of a room
Tips for Teaching
Because 7th grade requires use of nets to solve for total and lateral surface area, students are going to need a method for organizing their work. Sara, a member of our curriculum team, recommends, “Find the area of each face and write the area on the net, then students add up each face to find the total or lateral surface area.”
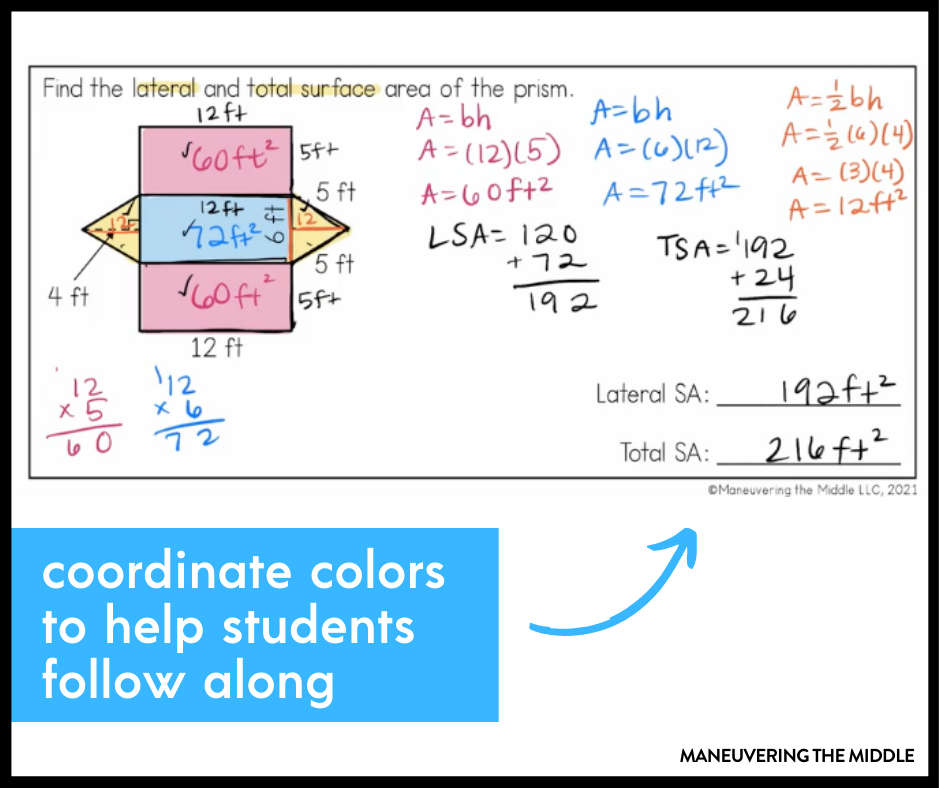
This is also helpful when it comes to grading because you can give credit to students who may have made a computation error on one of the faces, impacting their final answer. This may be enough motivation for students to show their work.
In the image above, the pen colors for the formulas and calculations match the shading for the corresponding faces. These are small things that can really help students follow along. (This image is a screen grab from our All Access Student Videos.)
You can also ask students to create a table to organize their work, similar to our Surface Area Student Handout 2 shown below.

8th Grade Formula Chart
For 8th grade, the STAAR reference sheet for surface area looks like this (outlined in green).
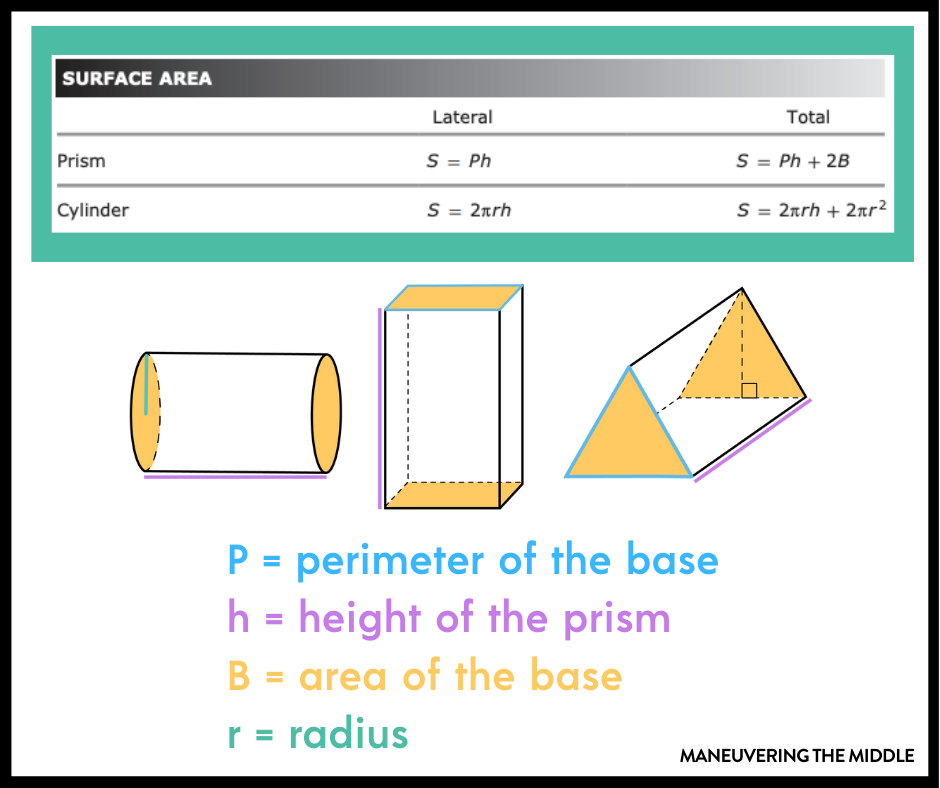
You will need to repeat the phrases, “perimeter of the base,” “area of the base” and “height of the prism” until you lose your voice. This is a great time to rapidly cold call students to ask what each variable represents.
Triangular and Rectangular Pyramids
Pyramids are included in 7th grade TEKS and 7th grade CCSS.
A pyramid is composed of a base and triangular faces. The pyramid is named by the shape of the base – so triangular prisms have a triangle base while rectangular pyramids have a square or rectangle as a base. Pyramids have one base and the lateral faces all come to one point, the vertex.
It is important to differentiate between the lateral height (which is the height of the triangular face) and the height of the pyramid. This will be an important distinction when they transition to calculating volume in later units.
Students sometimes struggled with differentiating between pyramids and triangular prisms. To help students, ask, “Are there more triangles or quadrilaterals?” If there are more triangles, then you have a pyramid. If there are more quadrilaterals, then you have a triangular prism.
Activity Ideas
1. Make it hands on
In 7th grade, surface area is a brand new concept, so students will need time to understand what surface area is. Reusing amazon boxes, cereal boxes, or cracker boxes can be a great exercise to make the connection between 3D figures and their nets. You can provide student groups with a 3D box, they measure the dimensions (length, width, height), and then carefully cut to form the rectangular prism’s net. They will see those same dimensions that form the box’s net.
In addition, bring in soup cans (cylinders) and peel off the label to show the rectangular face of a cylinder. It can be tricky for students to see how a rectangle fits on a cylinder’s net.
2. Digital Activities
Our 7th Grade Surface Area Digital Activities do a fantastic job of breaking down the nets (see below). Our 8th Grade Surface Area Digital Activities provide great application opportunities.
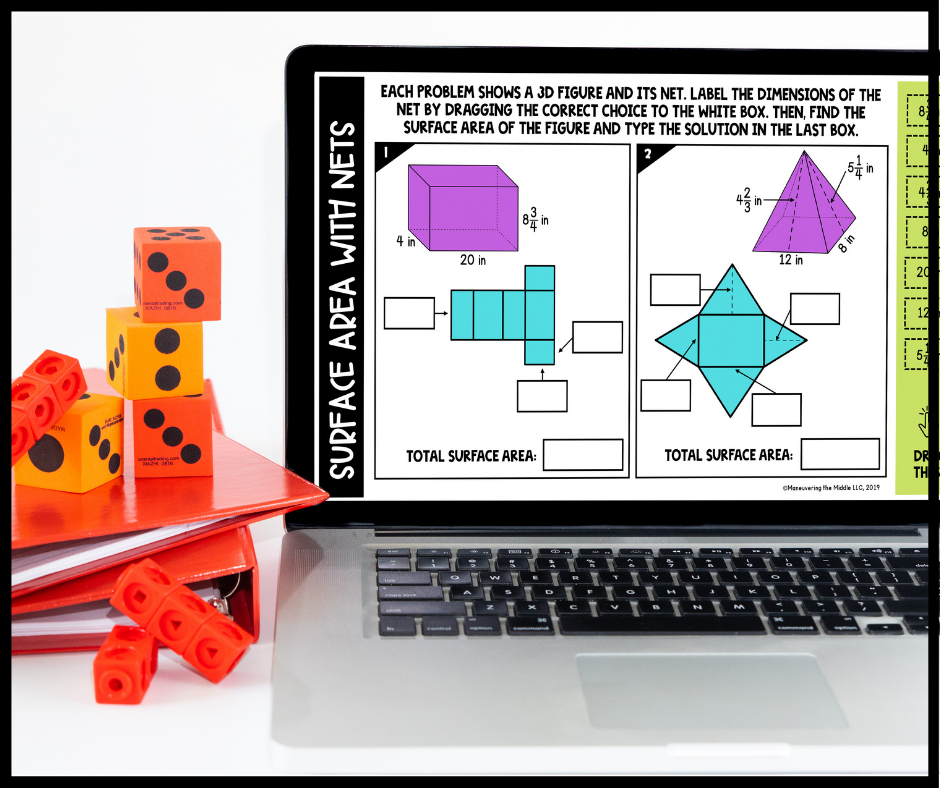
3. Change Up the Writing Utensil
Using formulas over and over again can be pretty repetitive. Allowing students to practice using dry erase markers or chalk outside is a great way to break it up.
4. Assess Creatively
This performance task activity is a great way to apply surface area.

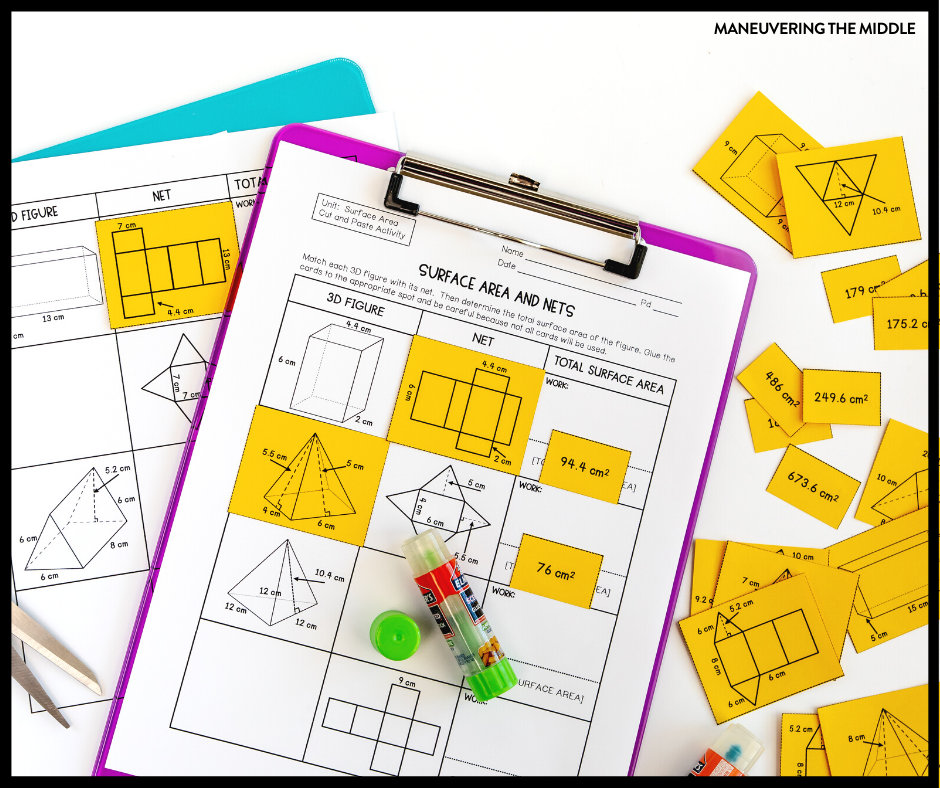
5. Match Nets to Shapes
This Surface Area and Nets Cut and Paste (no time to cut and glue? Just make it a matching activity) is perfect for students to practice matching nets with their corresponding 3D shape.
Common Misconceptions
There are quite a few, so let’s dig in:
- Assuming the base of the figure is the face is at the bottom. Make sure to emphasize that the base must be congruent and parallel for prisms and cylinders.
- I love this simple idea from a member of our curriculum team, Ashleigh, “Students assume the figure is always sitting on its base, so I would hold up a triangular prism (this one was hardest for them). I would lay it in my hand where it was “sitting” on the triangle. They would tell me it was a triangular prism. Then I would flip it over where it was laying on one of the rectangular faces and ask them what it was again. They would say it was still a triangular prism. This helped them see that no matter which way it was facing or which shape was on the bottom didn’t matter.”
- Using the formula, students will plug in a length or width of the base instead of the total area of the base. Our curriculum writers, Reagan and Asheigh, recommend always solving for the area of the base first and separately and clearly label it a B.
- Students think that height is always a vertical measurement. Height is perpendicular to the base no matter where the base sits.
- With triangular prisms, there are so many heights and so many bases. This can be so confusing! Avoid using the words “height” or “base” without saying “height of the triangle” or “height of the prism.” Base is now and forever “area of the base” and always solved first separately.
- When working with cylinders, students may confuse the diameter and the radius. Radius, as a word, is shorter than diameter which supported my reminder that the radius is half of its diameter.
What tips do you have for teaching surface area?