Comparing and ordering rational numbers is a complex skill with many steps, often complicated by the number of ways the problem can be presented. These tips and ideas will help scaffold this skill and make it more hands-on and engaging for your students.

Standards
Comparing and ordering rational numbers is predominantly a 6th grade skill in both Common Core and TEKS. It will also support students locating and plotting rational numbers on the coordinate plane.
- 6.NS.7 Understand ordering and absolute value of rational numbers.
- 6.2D Order a set of rational numbers arising from mathematical and real-world contexts (Readiness Standard)

Released Staar Question
Looking at a test question isn’t a way to “teach to the test,” but rather, a way for me to make sure that I am teaching the complexity of the standard. By looking at the test question above, it helps me to understand that:
- Students will need to order a set of 5 (or possibly more) rational numbers
- These rational numbers will vary in type (fractions, mixed numbers, improper fractions, whole numbers, and decimals) so I can assume that test questions can also include percentages
- It also helps me recognize that I need to make sure students pay attention to the order in which the question is asking
- Greatest to least – which can also include words like “descending”
- Least to greatest – which can also include words like “ascending”
Convert to the Same Form (fraction, decimal, percent)
Before you can jump into ordering rational numbers, you will need to spend a few days on converting between fractions, decimals, and percentages.
But I wouldn’t start by ordering a set of numbers that include fractions, decimals, and percentages. Start by scaffolding! Order a set of decimals, then a set of percentages, and lastly a set of fractions before introducing a mixed bag of rational numbers.
For decimals, I suggest asking students to line up the decimal point and compare the digits going from left to right.
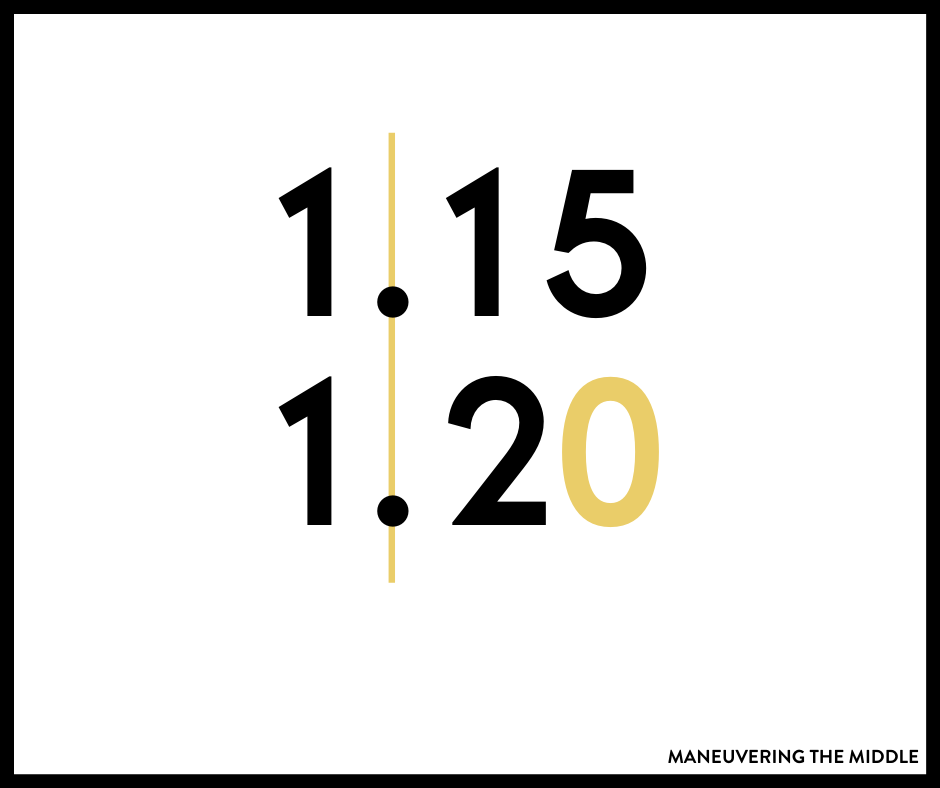
Have students add zeros to numbers after the decimal point so no student confuses a number with more digits as greater.
For percentages, I would use the same method. Remind students where the decimal point is in a percentage if it is not visible.
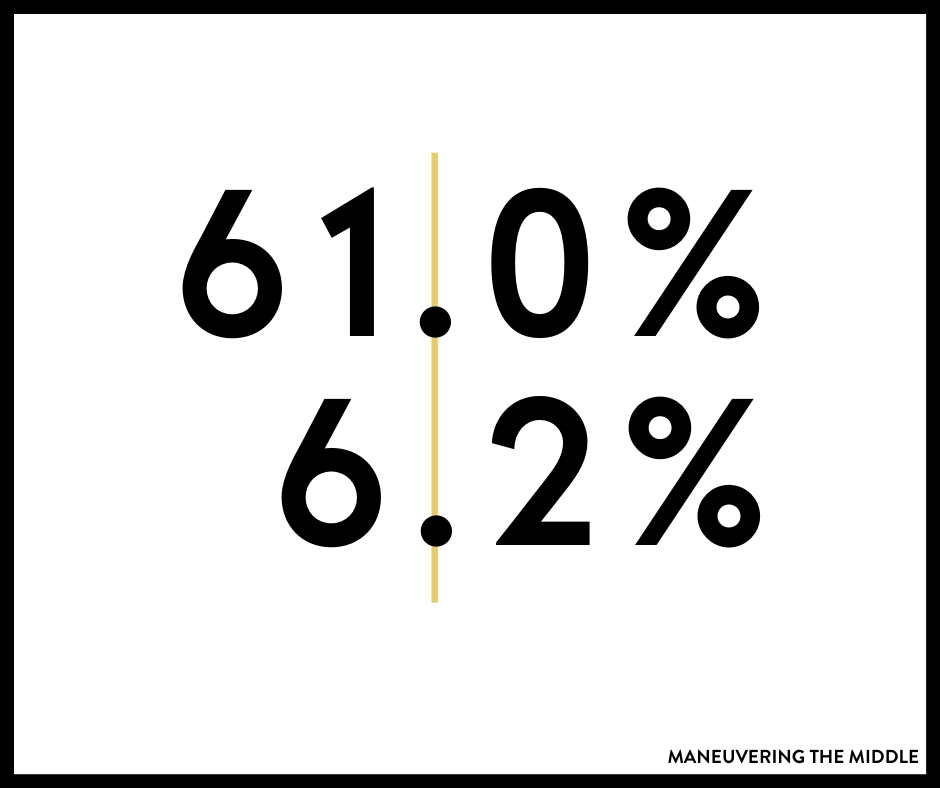
For fractions, this is where I don’t have strong opinions. Perhaps because I have not seen one method to be more successful than others. Butterfly method, finding a common denominator, converting fractions into a decimal, reasoning through it – I think each student will gravitate toward their favorite based on their past experiences.
Once students have mastered ordering from the same type of rational numbers, have students order a small set of 3 rational numbers by converting them to the same form. In my experience, students (and me, the teacher) like to convert most rational numbers to decimals. I think this is because they are the easiest to compare and then order.
Use a Number Line
When negative numbers are included, a number line is an absolute must. The number line gives us context! A quick sketch of a number line with a zero in the middle immediately serves as a reminder that the numbers with the least value will be the furthest left and the numbers with the greatest value will be the furthest right!
In fact, a number line was a requirement for work shown when we ordered numbers in class. A dry erase marker and a desk allowed for lots of space for converting between the fractions, decimals, and percentages and placing them on the number line.
Quick Hits
- Have a half day or need an extension activity? Have students make flashcards of benchmark fractions: ¼, ½, ¾, ⅕, ⅖, ⅗, ⅘. Once my students could ace this in a flyswatter challenge, I would add ⅛, ⅜, ⅝, ⅞. If students had these benchmark fractions memorized, it lightened the mental load for ordering rational numbers.
- Make ordering numbers hands on! This can be done by using these cards. Print a set, laminate, and then have a living number line using the sticky side of painter’s tape (see the idea here).
- Get students moving! Give each student a card with a rational number. Tell them to get into groups of 4 and stand in order from least to greatest. Then tell them to find a new group with 3 people and stand in order from greatest to least. Go around the room and listen to their reasoning. You can do this as many times as you want using a different number of students and in a different order. You can finish the activity by having all the students stand in ascending or descending order.
How do you teach comparing and ordering rational numbers?






There are some great ideas in here, but the percent trick just fuels misunderstandings about what a percent represents and its value. In addition, this will not work for the 8th grade standard where students are asked to order a mixed representation of rational numbers.